FRM Part Ⅰ: Quantitative Analysis

The Quantitative Analysis is Chapter 2 of Part 1 for the FRM exam. This chapter primarily covers probability and statistics, hypothesis testing and estimation, time series analysis, risk management and portfolio management, and derivatives and risk models.

Probability Theory

Fundamentals of Probability

1. 三个概率：条件概率，非条件概率，联合概率
2. 三个事件：互斥事件，独立事件，条件独立事件
3. 两个公式：全概率，贝叶斯

• Random experiment

  • An observation or measurement process with multiple but uncertain outcomes

• Sample Space

  • A set containing all possible outcomes of an experiment. E.g., the sample space of a rolling a single six-sided die is {1,2 …, 6}.

• Events

  • Subsets of sample space , i.e., a set of outcomes and may contain one - or more of the values in the sample space , or it may even contain no elements.

• Event Space

  • The event space consists of all combinations of outcomes

• Venn Diagrams

  

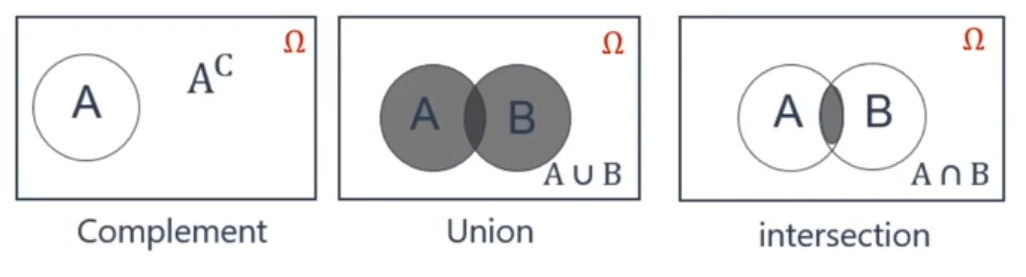
  补集

  并集： P(A U B) = P(A + B) = P(A or B)

  交集：P(A ∩ B) = P(AB) = P(A and B)

• Mutually exclusive events

  • Events that cannot both happen at the same time.

• Axioms of Probability

  • Any event A in the event space has P(A)≥0 or Pr(A)≥0
  • The probability of all events in sample space is 1
  • If events A1 and A2 are mutually exclusive, P(A1 ∪ A2)=P(A1)+P(A2)

• Extensions

  • The probability of an event or its complement must be 1

    $P(A∪A^c)=P(A)+P(A^C)=1$

  • The probability of the union of any two sets can be decomposed into:

    $P(A∪B)=P(A)+P(B)-P(A∩B)$

    $P(A+B)=P(A)+P(B)-P(AB)$

    $P(A or B)=P(A)+P(B)-P(A and B)$

Conditional probability

• Unconditional Probability(Marginal Probability) (非条件概率 或 边际概率：一件事发生不受其他因素影响)

  • The probability of an event without any restrictions (or lacking any prior information), commonly know as P(A)

• Conditional Probability

  • The probability on condition that another event occurs first. The conditional probability of event B, conditional on Event A, is given by

    $P(B|A)=\frac{P(A ∩ B)}{P(A)}; P(A) >$

Random Variables

Common Univariate Random Distributions

Multivariate Random Variables

Sample Moments

Mathematical Statistics

Hypothesis Testing

Linear Regression

Regression with Multiple Explanatory Variables

Regression Diagnostics

Time Series

Stationary Time Series

Non-Stationary Time Series

Measuring Returns,Volatility, and Correlation

Simulation Methods

Machine Learning

Machine-Learning Methods

Machine Learning and Prediction

To be continued…